6 Sezonowość

Jednym z rodzajów szeregu statystycznego jest szereg czasowy, który można zdefiniować jako ciąg obserwacji jakiegoś zjawiska w kolejnych jednostkach czasu (latach, kwartałach, miesiącach). Rozważane zjawisko może podlegać pewnym prawidłowościom, których wykrycie i opis jest celem analizy szeregów czasowych. Najczęściej rozważa się cztery czynniki wpływające na rozwój zjawiska w czasie:

trend ( $T_{t}$ ) — długookresowe, systematyczne zmiany, jakim podlega dane zjawisko,
wahania sezonowe ( $S_{t}$ ) — regularne odchylenia od tendencji rozwojowej (trendu) związane np. z porami roku (warunkami klimatycznymi),
wahania cykliczne ( $C_{t}$ ) — związane z cyklem koniunkturalnym,
wahania przypadkowe ( $I_{t}$ ) — nieregularne zmiany.

Analiza danych, które mogą charakteryzować się sezonowością rozpoczyna się od wizualizacji oraz estymacji parametrów modelu liniowego. W tym celu posłużymy się dwoma przykładami. Pierwszy będzie dotyczył zużycia energii elektrycznej, a drugi przewozów ładunków w Polsce - plik.

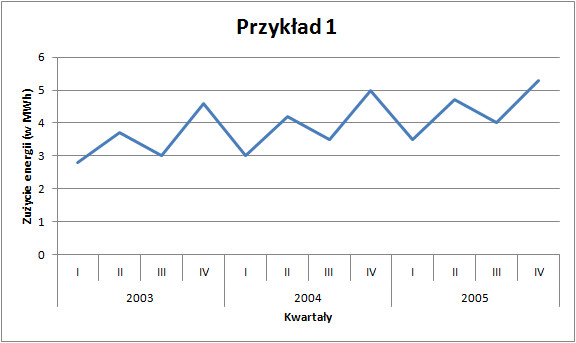
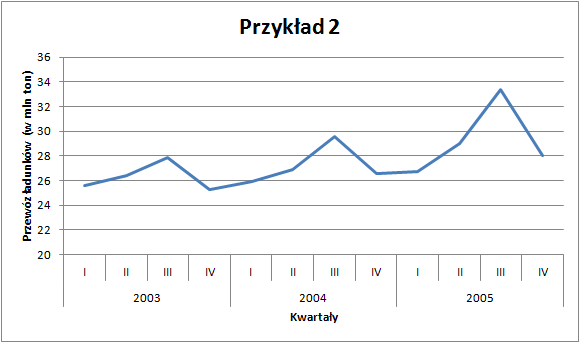
W obu przypadkach dysponujemy danymi kwartalnymi za lata 2003–2005. Na pierwszy rzut oka możemy wskazać pewne prawidłowości: zużycie energii jest widocznie wyższe w drugich i czwartych kwartałach analizowanych lat. Z kolei przewozy ładunków wzrastają od kwartału pierwszego do trzeciego (w którym osiągają maksimum w danym roku), by następnie spaść.

Celem analizy będzie ilościowe określenie wielkości zmian sezonowych, tak aby było możliwe prognozowanie z uwzględnieniem tych czynników.

6.1 Trend liniowy

Pierwszym krokiem w analizie szeregu czasowego jest estymacja parametrów trendu liniowego.

Dla przykładu pierwszego dotyczącego zużycia energii funkcja regresji przyjmuje następującą postać:

${\hat{y}}_{t} = 0, 15 \cdot t + 2, 99$

w której współczynnik kierunkowy informuje o tym, że z kwartału na kwartał zużycie energii rosło przeciętnie o 0,15 MWh. Z kolei wyraz wolny równy 2,99 oznacza, że w okresie $t = 0$ czyli w IV kwartale 2002 roku, teoretyczne zużycie energii wynosiło 2,99 MWh.

W drugim z analizowanych przykładów — przewozów ładunków — model wyglądał następująco:

${\hat{y}}_{t} = 0, 38 \cdot t + 25, 13$

co oznacza, że z kwartału na kwartał przewóz ładunków wzrastał średnio o 0,38 mln ton, natomiast w IV kwartale 2002 roku modelowa wartość przewozów ładunków wynosiła 25,13 mln ton.

Na podstawie wyznaczonych funkcji regresji można obliczyć wartości teoretyczne ( ${\hat{y}}_{t}$ ) zużycia energii oraz przewozów ładunków i pod postacią prostej przestawić na wykresie.

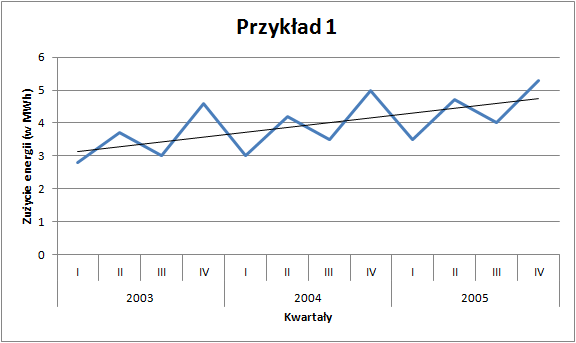
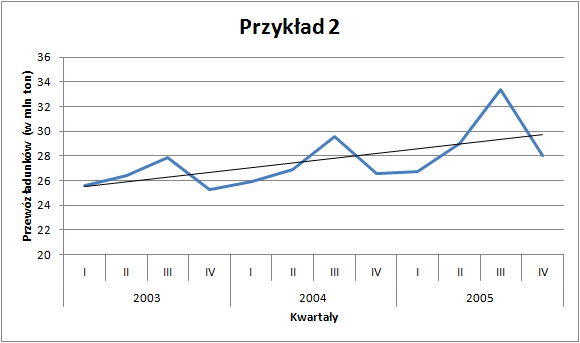
Zużycie energii - trend liniowy Przewóz ładunków - trend ilniowy

Otrzymane wartości wynikające z funkcji trendu ( ${\hat{y}}_{t}$ ) mają charakter liniowy i prawdę rzecz ujmując słabo dopasowują się do danych empirycznych. Współczynnik $R^{2}$ w przykładzie pierwszym wynosi 41%, a w przykładzie drugim tylko 37%. Ponadto, jeśli chcielibyśmy prognozować na kolejne okresy to według funkcji trendu wartości zużycia energii dla kwartałów pierwszych byłyby przeszacowane, a dla kwartałów czwartych niedoszacowane. Stąd zachodzi potrzeba uwzględnienia w modelu występowania sezonowości, którą obserwujemy w danych.

Pierwszym krokiem jest identyfikacja rodzaju tej sezonowości. Może ona mieć charakter addytywny — wtedy wahania sezonowe są stałe w poszczególnych okresach (por. przykład 1) lub multiplikatywny, kiedy czynniki sezonowe są proporcjonalne do funkcji trendu (por. przykład 2). W zależności od zidentyfikowanego charakteru należy obliczyć wskaźniki sezonowości. W pierwszej kolejności rozważymy model addytywny.

6.2 Model addytywny

Analizę modelu addytywnego należy rozpocząć od wyznaczenia różnic pomiędzy wartościami empirycznymi ( $y$ ) a modelowymi ( $\hat{y}$ ) dla poszczególnych okresów zgodnie ze wzorem:

$S_{t}^{i} = y_{t} - {\hat{y}}_{t}$

Następnie dla każdego z analizowanych podokresów (półroczy, kwartałów, miesięcy) oblicza się surowe wskaźniki sezonowości uśredniając wyznaczone wcześniej różnice:

$S_{i} = \frac{\sum_{i = 1}^{m} S_{t}^{i}}{p}$

gdzie:

$m$ — liczba podokresów (półroczy, kwartałów, miesięcy),
$p$ — liczba analizowanych lat.

W analizowanym przez nas przykładzie musimy wyznaczyć surowe wskaźniki sezonowości dla każdego kwartału. Ponadto jeśli spełniona będzie zależność $\sum_{i = 1}^{m} S_{i} = 0$ to oznacza, że wskaźniki sezonowości są wolne od wahań przypadkowych. W praktyce jednak rzadko zdarza się taka sytuacja. W takim przypadku należy jeszcze wyznaczyć współczynnik korygujący zgodnie z wzorem:

$k = \frac{\sum_{i = 1}^{m} S_{i}}{m}$

a następnie skorygować surowe wskaźniki sezonowości według formuły

$S o_{i} = S_{i} - k$

otrzymując tzw. oczyszczone wskaźniki sezonowości, które informują o średnich odchyleniach od funkcji trendu w poszczególnych podokresach. Dla tych wskaźników zachodzi zależność: $\sum_{i = 1}^{m} S o_{i} = 0$ . W przykładzie 1 oczyszczone wskaźniki sezonowości dla poszczególnych kwartałów są równe:

Wskaźnik	Wartość	Interpretacja
$S o_{1}$	-0,62	w pierwszych kwartałach lat 2003–2005 zużycie energii było mniejsze średnio o 0,62 MWh niż wynika to z funkcji trendu
$S o_{2}$	0,33	w drugich kwartałach lat 2003–2005 zużycie energii było większe średnio o 0,33 MWh niż wynika to z funkcji trendu
$S o_{3}$	-0,51	w trzecich kwartałach lat 2003–2005 zużycie energii było mniejsze średnio o 0,51 MWh niż wynika to z funkcji trendu
$S o_{4}$	0,81	w czwartych kwartałach lat 2003–2005 zużycie energii było większe średnio o 0,81 MWh niż wynika to z funkcji trendu
Suma	0,00	wskaźniki sezonowości są wolne od wahań przypadkowych

Kolejnym etapem analizy jest wyznaczenie zmodyfikowanych wartości teoretycznych uwzględniających sezonowość. Te wartości oznaczane jako ${\hat{y}}^{*}$ uzyskujemy dodając do wartości teoretycznych ( $\hat{y}$ ) odpowiednie dla poszczególnych podokresów oczyszczone wskaźniki sezonowości $S o_{i}$ . Formalny zapis jest następujący:

${\hat{y}}^{*} = \hat{y} + S o_{i}$

Wartości ${\hat{y}}^{*}$ przedstawione na wykresie już znacznie lepiej pasują do posiadanych danych empirycznych:

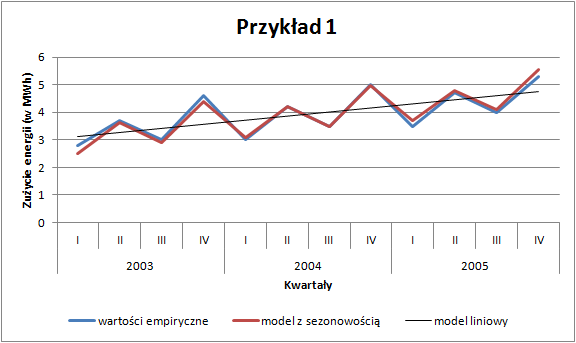
Na podstawie tak zmodyfikowanego modelu można prognozować przyszłe wartości z dużo większą precyzją. Prognozowanie w modelu addytywnym polega na podstawieniu numeru okresu dla którego się prognozuje do funkcji trendu, a następnie dodanie odpowiedniego wskaźnika sezonowości:

${\hat{y}}_{T}^{P} = \hat{y} + S o_{i} = a_{1} \cdot T + a_{0} + S o_{i}$

Interesuje nas prognozowane zużycie energii w IV kwartale 2008 roku. Ten okres przyjmuje wartość $t = 24$ , natomiast wskaźnik sezonowości dla czwartego kwartału jest równy 0,81 MWh. Powyższe wartości podstawiamy do wzoru:

${\hat{y}}_{24}^{P} = 0, 15 \cdot 24 + 2, 99 + 0, 81 = 7, 4$

co oznacza, że prognozowane zużycie energii w IV kwartale 2008 roku wyniesie 7,4 MWh.

6.3 Model multiplikatywny

W modelu multiplikatywnym zamiast różnic pomiędzy wartościami teoretycznymi a modelowymi oblicza się ich iloraz zgodnie ze wzorem:

$S_{t}^{i} = \frac{y_{t}}{{\hat{y}}_{t}}$

Następnie dla każdego z analizowanych podokresów (półroczy, kwartałów, miesięcy) oblicza się surowe wskaźniki sezonowości uśredniając wyznaczone wcześniej ilorazy:

$S_{i} = \frac{\sum_{i = 1}^{m} S_{t}^{i}}{p}$

gdzie:

$m$ — liczba podokresów (półroczy, kwartałów, miesięcy),
$p$ — liczba analizowanych lat.

W analizowanym przez nas przykładzie musimy wyznaczyć surowe wskaźniki sezonowości dla każdego kwartału. W przypadku sezonowości multiplikatywnej zależność oznaczająca, że wskaźniki sezonowości są wolne od wahań przypadkowych jest wyrażona następująco: $\sum_{i = 1}^{m} S_{i} = m$ . W praktyce jednak rzadko zdarza się taka sytuacja. W takim przypadku należy jeszcze wyznaczyć współczynnik korygujący zgodnie z wzorem:

$k = \frac{\sum_{i = 1}^{m} S_{i}}{m}$

a następnie skorygować surowe wskaźniki sezonowości według formuły

$S o_{i} = S_{i} / k$

otrzymując tzw. oczyszczone wskaźniki sezonowości, które informują o średnich odchyleniach od funkcji trendu w poszczególnych podokresach. Dla tych wskaźników zachodzi zależność: $\sum_{i = 1}^{m} S o_{i} = m$ . W przykładzie 2 oczyszczone wskaźniki sezonowości możemy zapisać w postaci procentowej i dla poszczególnych kwartałów są równe:

Wskaźnik	Wartość	Interpretacja
$S o_{1}$	96,5%	w pierwszych kwartałach lat 2003–2005 rzeczywiste przewozy były średnio o 3,5% niższe niż wynika to z funkcji trendu
$S o_{2}$	100,1%	w drugich kwartałach lat 2003–2005 rzeczywiste przewozy były średnio o 0,1% wyższe niż wynika to z funkcji trendu
$S o_{3}$	108,9%	w trzecich kwartałach lat 2003–2005 rzeczywiste przewozy były średnio o 8,9% wyższe niż wynika to z funkcji trendu
$S o_{4}$	94,5%	w czwartych kwartałach lat 2003–2005 rzeczywiste przewozy były średnio o 5,5% niższe niż wynika to z funkcji trendu
Suma	400,00%	wskaźniki sezonowości są wolne od wahań przypadkowych

Kolejnym etapem analizy jest wyznaczenie zmodyfikowanych wartości teoretycznych uwzględniających sezonowość. Te wartości oznaczane jako ${\hat{y}}^{*}$ uzyskujemy mnożąc wartości teoretyczne ( $\hat{y}$ ) odpowiednie dla poszczególnych podokresów przez oczyszczone wskaźniki sezonowości $S o_{i}$ . Formalny zapis jest następujący:

${\hat{y}}^{*} = \hat{y} \cdot S o_{i}$

Wartości ${\hat{y}}^{*}$ przedstawione na wykresie już znacznie lepiej pasują do posiadanych danych empirycznych:

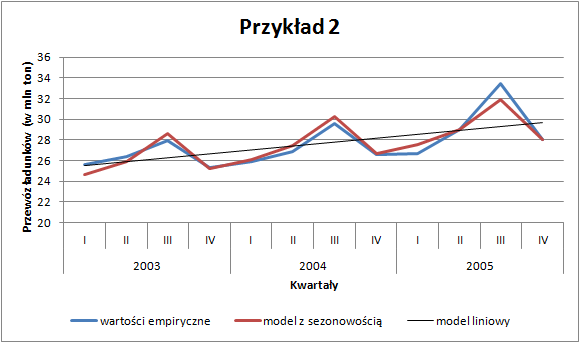
Na podstawie tak zmodyfikowanego modelu można prognozować przyszłe wartości z dużo większą precyzją. Prognozowanie w modelu multiplikatywnym polega na podstawieniu numeru okresu dla którego się prognozuje do funkcji trendu, a następnie przemnożenie przez odpowiedni wskaźnik sezonowości:

${\hat{y}}_{T}^{P} = \hat{y} \cdot S o_{i} = (a_{1} \cdot T + a_{0}) \cdot S o_{i}$

Interesuje nas prognozowane zużycie energii w III kwartale 2006 roku. Ten okres przyjmuje wartość $t = 15$ , natomiast wskaźnik sezonowości dla kwartału trzeciego jest równy 108,9%. Powyższe wartości podstawiamy do wzoru:

${\hat{y}}_{15}^{P} = (0, 38 \cdot 15 + 25, 13) \cdot 108, 9 % = 33, 6$

co oznacza, że prognozowane przewozy ładunków w III kwartale 2006 roku wyniosą 33,6 mln ton.

6.4 Ocena jakości

Ostatnim elementem analizy sezonowości jest ocena jakości otrzymanego modelu. W takim przypadku nie wyznaczamy współczynnika $R^{2}$ ponieważ z definicji dotyczy on wyłącznie zależności liniowej. Główną miarą jakości będzie odchylenie standardowe składnika resztowego z uwzględnieniem sezonowości:

$S_{u}^{*} = \sqrt{\frac{\sum_{t = 1}^{n} (y_{t} - {\hat{y}}_{t}^{*})^{2}}{n - 2}}$

Licznik odchylenia standardowego zawiera sumę kwadratów odchyleń wartości empirycznych ( $y_{t}$ ) od wartości modelowych z sezonowością ( ${\hat{y}}_{t}^{*}$ ). Nie ma już tutaj znaczenia czy model był addytywny czy multiplikatywny.

W przykładzie pierwszym $S_{u}^{*}$ wynosiło 0,16 MWh, co oznacza, że rzeczywiste zużycie energii różni się od zużycia teoretycznego wyznaczonego na podstawie szeregu czasowego średnio o +/- 0,16 MWh. Z kolei w przykładzie drugim $S_{u}^{*}$ wynosiło 0,74 mln ton, a co za tym idzie rzeczywiste przewozy różnią się od przewozów teoretycznych uzyskanych w oparciu o model szeregu czasowego średnio o +/- 0,74 mln ton.

6.5 Błąd prognozy

Wyliczona wartość $S_{u}^{*}$ niezbędna jest przy wyznaczaniu błędu prognozy zgodnie ze wzorem:

$D (y_{T}^{P}) = S_{u}^{*} \sqrt{1 + \frac{1}{n} + \frac{(T - \bar{t})^{2}}{\sum_{t = 1}^{n} (t - \bar{t})^{2}}}$

w którym uwzględniamy możliwość wzrostu tego błędu wraz z oddalaniem się od zakresu danych, które posiadamy.

Dla analizowanych przykładów otrzymano następujące błędy prognozy:

przykład 1 — zużycie energii

Przy prognozie dla IV kwartału 2008 roku

$D (y_{24}^{P}) = 0, 29$

co oznacza, że prognozowane zużycie energii w IV kwartale 2008 roku wyniesie 7,4 +/- 0,29 MWh. - przykład 2 — przewóz ładunków

Przy prognozie dla III kwartału 2006 roku

$D (y_{24}^{P}) = 0, 93$

co oznacza, że prognozowane przewozy w III kwartale 2006 roku wyniosą 33,6 +/- 0,93 mln ton.

Na podstawie otrzymanych prognoz oraz ich błędów można wyznaczyć przedziały, w których spodziewamy się wartości rzeczywistej.