Metoda reprezentacyjna

class: center, middle, inverse, title-slide

# Metoda reprezentacyjna
## Minimalna liczebność próby
### © Łukasz Wawrowski

---

# Wprowadzenie

Link do ankiet: https://pollev.com/lukaszw470

---

---

---

---

# Minimalna liczebność próby

Minimalna liczebność próby (MLP) informuje ile jednostek należy przebadać, aby maksymalny błąd oszacowania (na poziomie ufności `$1–\alpha$`) wyniósł co najwyżej `$d$`.

Przy większej liczbie jednostek oszacowanie będzie bardziej trafne (przedział ufności będzie węższy). Z drugiej strony koszty badania rosną wraz ze wzrostem liczebności próby.

Szukamy kompromisu pomiędzy dokładnością, a liczbą badanych jednostek.

Wyznaczoną wartość zawsze zaokrąglamy w górę.

---

# Podejście kosztowe

Badane jest tyle jednostek na ile pozwala założony budżet.

`$$n = \frac{\text{budżet} - \text{koszty stałe}}{\text{koszt jednostkowy}}$$`

Przykład:

`$$n=\frac{25000-5000}{20}=1000$$`

W tym podejściu nie bierzemy pod uwagę błędu oszacowania.

---

## Podejścia oparte o przedział ufności

Do wyznaczenia minimalnej liczebności niezbędne jest ustalenie:

- poziomu istotności (i związanego z nim poziomu prawdopodobieństwa) - `$\alpha$`
- maksymalnego dopuszczalnego błędu pomiaru - `$d$`
- odsetek/odchylenie standardowe z badania pilotażowego - `$p_0$` lub `$\sigma$`

Zakładamy, że wielkość populacji jest nieskończona - nie wpływa to znacząco na wyniki, a upraszcza obliczenia.

[Kalkulator minimalnej liczebności próby](https://www.statystyka.az.pl/dobor/kalkulator-wielkosci-proby.php)

---

# Przedział ufności dla średniej

`$$P\left\{\bar{X}-z_{(1-\alpha/2)}\frac{\sigma}{\sqrt{n}}<m<\bar{X}+z_{(1-\alpha/2)}\frac{\sigma}{\sqrt{n}}\right\}=1-\alpha$$`
gdzie:

- `$m$` - prawdziwa wartość średniej w populacji,
- `$\bar{X}$` - estymator średniej z próby,
- `$z_{(1-\alpha/2)}$` - kwantyl rozkładu normalnego obliczony dla poziomu istotności `$\alpha$`,
- `$\sigma$` - znane odchylenie standardowe,
- `$n$` - liczebność próby.

Błąd oszacowania to wynik odejmowania i dodawania od i do średniej z próby.

Przykładowo: przedział ufności czasu pracy w ciągu tygodnia wynosi `$(35,45)$` godzin. Zatem średnia z próby wynosi 40 godzin, a błąd 5 godzin.

---

### MLP - wyprowadzenie

`$$P\left\{\bar{X}-z_{(1-\alpha/2)}\frac{\sigma}{\sqrt{n}}<m<\bar{X}+z_{(1-\alpha/2)}\frac{\sigma}{\sqrt{n}}\right\}=1-\alpha$$`
Za błąd odpowiada:

`$$z_{(1-\alpha/2)}\frac{\sigma}{\sqrt{n}}$$`

Chcemy, żeby błąd był mniejszy od tego wyrażenia:

`$$d \geq z_{(1-\alpha/2)}\frac{\sigma}{\sqrt{n}}$$`
Zatem po przekształceniach:

`$$\sqrt{n} \geq z_{(1-\alpha/2)}\frac{\sigma}{d}$$`
Otrzymujemy wzór na minimalną liczebność próby:

`$$n \geq \left(z_{(1-\alpha/2)}\frac{\sigma}{d}\right)^2$$`

---

# MLP - szacowanie średniej (I)

Znane odchylenie standardowe w populacji.

`$$n \geq \left(z_{(1-\alpha/2)} \cdot \frac{\sigma}{d}\right)^2$$`

gdzie:

- `$z_{1-\alpha/2}$` - kwantyl rozkładu normalnego obliczony dla poziomu istotności `$\alpha$`
- `$\sigma$` - odchylenie standardowe w populacji
- `$d$` - maksymalny dopuszczalny błąd pomiaru

---

# MLP - szacowanie średniej (II)

Nieznane odchylenie standardowe w populacji.

`$$n \geq \left(t_{(1-\alpha/2,n_0-1)} \cdot \frac{s}{d}\right)^2$$`

gdzie:

- `$t_{(1-\alpha/2,n_0-1)}$` - kwantyl rozkładu t-Studenta obliczony dla poziomu istotności `$\alpha$` i dla stopni swobody `$n_0-1$`
- `$n_0$` - wielkość próby w badaniu pilotażowym
- `$s$` - odchylenie standardowe w badaniu pilotażowym
- `$d$` - maksymalny dopuszczalny błąd pomiaru

---

# MLP - szacowanie odsetka (I)

Znany szacunkowy odsetek.

`$$n \geq z_{(1-\alpha/2)}^2 \cdot \frac{p_0(1-p_0)}{d^2}$$`

gdzie:

- `$z_{1-\alpha/2}$` - kwantyl rozkładu normalnego obliczony dla poziomu istotności `$\alpha$`
- `$p_0$` - znany szacunkowy odsetek
- `$d$` - maksymalny dopuszczalny błąd pomiaru

---

# MLP - szacowanie odsetka (II)

Nieznany szacunkowy odsetek.

`$$n \geq z_{(1-\alpha/2)}^2 \cdot \frac{1}{d^2}$$`

gdzie:

- `$z_{1-\alpha/2}$` - kwantyl rozkładu normalnego obliczony dla poziomu istotności `$\alpha$`
- `$d$` - maksymalny dopuszczalny błąd pomiaru

---

# Wartości kwantyli N(0,1)

| Prawdopodobieństwo | Poziom istotności | Kwantyl rozkł. norm.|
|-------------------:|------------------:|--------------------:|
| 99% (0,99) | 0,01 | 2,58 | 
| 95% (0,95) | 0,05 | 1,96 |
| 90% (0,90) | 0,10 | 1,64 |

Wyznaczanie wartości kwantyli w R:

- `qnorm(p = 1-alfa/2)`
- `qt(p = 1-alfa/2, df = n0-1)`

Wyznaczanie wartości kwantyli w Excelu:

- `ROZKŁ.NORMALNY.S.ODWR(1-alfa/2)`
- `ROZKŁ.T.ODWR(1-alfa/2;n0-1)` lub `ROZKŁ.T.ODWR.DS(alfa;n0-1)`

Wyznaczanie wartości kwantyli w Google Sheets:

- `NORMSINV(1-alfa/2)`
- `TINV(alfa, n0-1)`

---

# Przykładowe wartości

![](img/mlp.png)

[źródło](http://www.tools4dev.org/resources/how-to-choose-a-sample-size/)

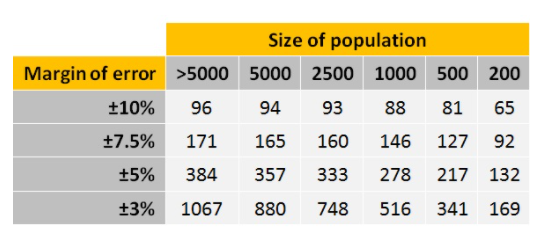
Uzyskane wielkości dotyczą populacji ogółem. Jeżeli chcemy przedstawić wyniki np. w podziale miasto/wieś to należy MLP pomnożyć przez 2, a dla wykształcenia (podstawowe/średnie/wyższe) przez 3, itd.

---

# MLP - szacowanie odsetka (I)

![](03_liczebnosc_proby_files/figure-html/unnamed-chunk-2-1.png)

---

# MLP - maksymalne wartości

|    d| alfa| maksimum_n|
|----:|----:|----------:|
| 0.01| 0.01|      16588|
| 0.01| 0.05|       9604|
| 0.01| 0.10|       6764|
| 0.03| 0.01|       1844|
| 0.03| 0.05|       1068|
| 0.03| 0.10|        752|
| 0.05| 0.01|        664|
| 0.05| 0.05|        385|
| 0.05| 0.10|        271|

---

# Przykład

Chcemy oszacować odsetek mieszkańców Poznania, którzy są zadowoleni z życia zakładając błąd badania równy 3% i prawdopodobieństwo 95%.

Według Badania Spójności Społecznej w 2018 roku zadowolonych z życia było 73% polaków [(GUS 2020) ](https://stat.gov.pl/obszary-tematyczne/warunki-zycia/dochody-wydatki-i-warunki-zycia-ludnosci/jakosc-zycia-i-kapital-spoleczny-w-polsce-wyniki-badania-spojnosci-spolecznej-2018,4,3.html)

---

# Dane

- błąd badania `$d$`: 0.03

- prawdopodobieństwo: 0.95

- alfa: 1 - 0.95 = 0.05

- szacunkowy odsetek `$p_0$`: 0.73

---

# Eksperyment z losowaniem

1. Generujemy wektor zawierający odpowiedzi w populacji `$N$`

2. Losujemy próbę o wielkości `$n$`

3. Sprawdzamy czy w wylosowanej próbie odpowiedzi są takie jak w populacji

---

# Losowanie próby

```r
set.seed(123)

N <- 535946
m <- round(0.73*N)

zadowoleni <- rep(1, m)
niezadowoleni <- rep(0, N-m)

populacja <- c(zadowoleni, niezadowoleni)

summary(populacja)
```

```
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    0.00    0.00    1.00    0.73    1.00    1.00
```

```r
n <- 842

proba <- sample(x = populacja, size = n)

mean(proba)
```

```
## [1] 0.719715
```

---

### Symulacja wielokrotnego losowania

```r
wyniki <- numeric(1000)

for(losowanie in 1:1000){
  
  proba <- sample(x = populacja, size = n)
  
  wyniki[losowanie] <- mean(proba)
  
}

summary(wyniki)
```

```
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##  0.6805  0.7197  0.7304  0.7296  0.7387  0.7767
```

```r
mean(wyniki > 0.7 & wyniki < 0.76)
```

```
## [1] 0.954
```

---

### MLP w badaniu gospodarstw domowych

[Designing Household Survey Samples: Practical Guidelines](https://unstats.un.org/unsd/demographic/sources/surveys/Handbook23June05.pdf)

`$$n_h\geq\frac{z_{1-\alpha/2}^2p_0(1-p_0)fk}{p\bar{n}d^2}$$`

- `$z_{1-\alpha/2}$` - kwantyl rozkładu normalnego obliczony dla poziomu istotności `$\alpha$`
- `$p_0$` - znany szacunkowy odsetek
- `$f$` - efekt metody doboru próby (domyślnie 2)
- `$k$` - mnożnik uwzględniający wskaźnik braków odpowiedzi
- `$p$` - odsetek populacji, którego dotyczy `$p_0$`
- `$\bar{n}$` - średnia wielkość gospodarstwa 
- `$d$` - maksymalny dopuszczalny błąd pomiaru

---

---

---

---

class: inverse, center, middle

# Pytania?