class: center, middle, inverse, title-slide .title[ # Metody przetwarzania<br>i analizy danych ] .subtitle[ ## Regresja liniowa ] .author[ ### © Łukasz Wawrowski ] --- # Regresja Funkcyjne odwzorowanie zależności pomiędzy badanymi zmiennymi. Cele analizy regresji: - poznawcze - badanie związków przyczynowo-skutkowych - predykcyjne - oszacowanie nieznanej wartości cechy Model regresji jest tylko przybliżeniem rzeczywistości! --- # Regresja prosta Analiza dwóch cech: - zmienna objaśniana (zależna) oznaczana jako `\(y\)` - zmienna objaśniająca (niezależna) oznaczana jako `\(x\)` Przykłady: - zależność wielkości sprzedaży od wydatków na reklamę - zależność wynagrodzenia od lat doświadczenia --- # Przykład Zbiór [salary](http://www.wawrowski.edu.pl/data/salary.xlsx) zawiera informacje o rocznym wynagrodzeniu (w $) oraz liczbie lat doświadczenia. 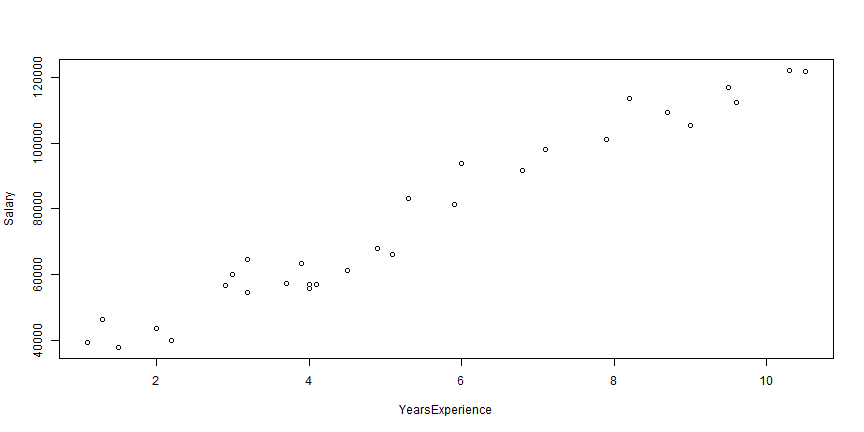--- # Wykres rozrzutu <!-- --> --- class: inverse # Zadanie Stwórz wykres rozrzutu dla zbioru `salary` z wykorzystaniem pakietu _ggplot2_. <div class="countdown" id="timer_7c616924" data-update-every="1" tabindex="0" style="top:0;right:0;"> <div class="countdown-controls"><button class="countdown-bump-down">−</button><button class="countdown-bump-up">+</button></div> <code class="countdown-time"><span class="countdown-digits minutes">05</span><span class="countdown-digits colon">:</span><span class="countdown-digits seconds">00</span></code> </div> --- # Wykres rozrzutu <!-- --> --- # 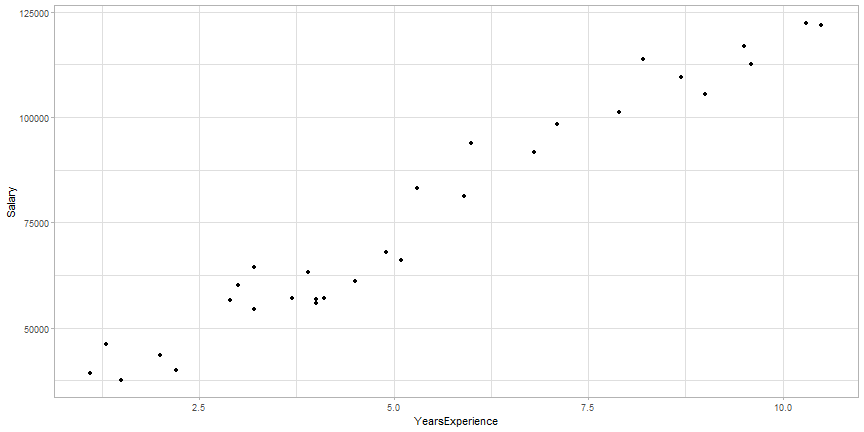Wykres rozrzutu <!-- --> --- # 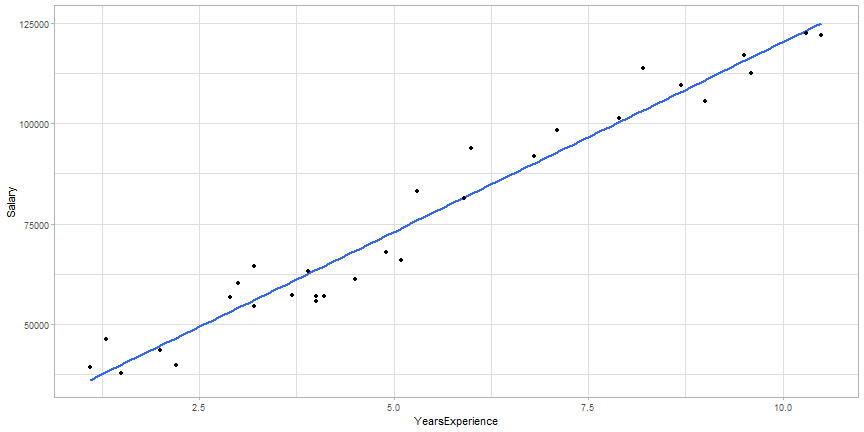Regresja prosta Weźmy pod uwagę prosty przykład dochodów i wydatków: | wydatki| dochody| |-------:|-------:| | 2300| 2600| | 1800| 2400| | 2400| 2900| | 2300| 2800| | 2800| 3000| | 2000| 2500| | 2100| 2700| --- # Regresja prosta Wykres rozrzutu <!-- --> --- # 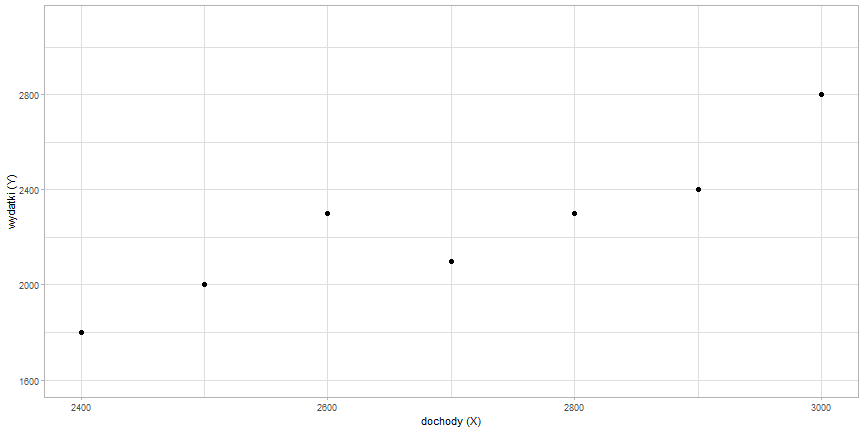Regresja prosta Spróbujmy teraz dopasować kilka prostych - mogą one przebiegać na wiele różnych sposobów. 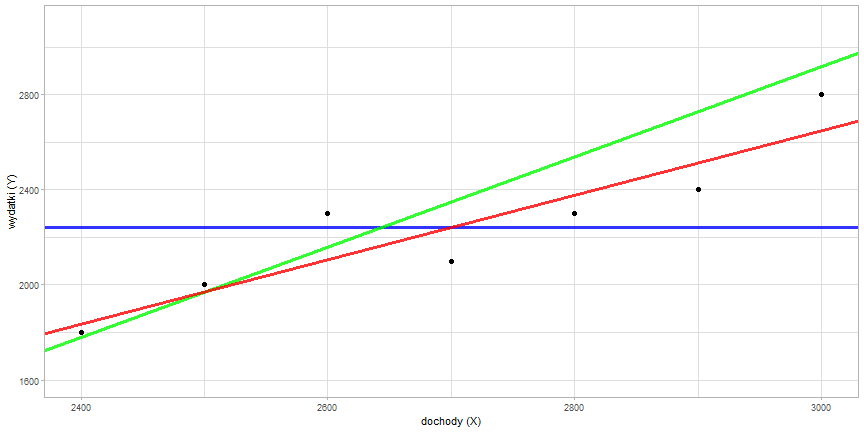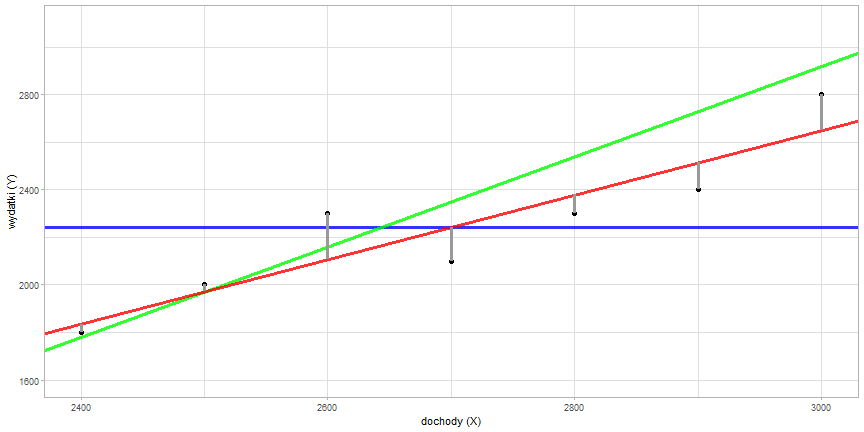<!-- --> --- # Regresja prosta W następnym kroku obliczamy różnice pomiędzy istniejącymi punktami, a odpowiadającym im wartościom na prostej: <!-- --> --- # Regresja prosta Oznaczając `\(y_i\)` jako rzeczywista wartość wydatków i `\(\hat{y_i}\)` jako wartość leżącą na prostej zależy nam na minimalizowaniu wyrażenia `\(\sum\limits_{i=1}^{n}{(y_{i}-\hat{y}_{i})^2} \rightarrow min\)`. Różnica `\(y_{i}-\hat{y}_{i}\)` jest nazywana resztą (ang. residual). Wyznaczając te wartości dla analizowanych przez nas prostych otrzymamy następujące wyniki: |name | suma_kwadratow_reszt| |:---------|--------------------:| |czerwona | 101430| |zielona | 264300| |niebieska | 22462143| --- # Regresja prosta Ogólna postać regresji prostej jest następująca: `$$\hat{y}_{i}=b_{1}x_{i}+b_{0}$$` gdzie `\(\hat{y}\)` oznacza wartość teoretyczną, leżącą na wyznaczonej prostej. Wobec tego wartości empiryczne (y) będą opisane formułą: `$$y_{i}=b_{1}x_{i}+b_{0}+u_{i}$$` w której `\(u_i\)` oznacza składnik resztowy wyliczany jako `\(u_{i}=y_{i}-\hat{y}_{i}\)`. --- # Regresja prosta w R ```r lm(formula = zmienna_zalezna ~ zmienna_niezalezna, data = zbior_danych) ``` - `formula` - zdefiniowanie zależności funkcyjnej z wykorzystaniem tyldy - `data` - zbiór danych Domyślnie funkcja `lm` zwraca tylko parametry `\(b\)`. Aby uzyskać szczegółowe informacje na temat modelu należy dodatkowo zastosować funkcję `summary()`: ```r model <- lm(formula = zmienna_zalezna ~ zmienna_niezalezna, data = zbior_danych) summary(model) ``` --- # Współczynniki `\(b\)` **Współczynnik kierunkowy** `\(b_1\)` informuje o ile przeciętne zmieni się wartość zmiennej objaśnianej `\(y\)`, gdy wartość zmiennej objaśniającej `\(x\)` wzrośnie o jednostkę. **Wyraz wolny** `\(b_0\)` to wartość zmiennej objaśnianej `\(y\)`, w sytuacji w której wartość zmiennej objaśniającej `\(x\)` będzie równa 0. Często interpretacja tego parametru nie ma sensu. --- # Dopasowanie modelu **Odchylenie standardowe składnika resztowego** jest pierwiastkiem z sumy kwadratów reszt podzielonej przez liczbę obserwacji pomniejszoną o 2: `$$S_{u}=\sqrt{\frac{\sum\limits_{i=1}^{n}{(y_{i}-\hat{y}_{i})^2}}{n-2}}$$` Miara ta określa, o ile, przeciętnie biorąc `\(+/-\)`, wartości empiryczne zmiennej objaśnianej odchylają się od wartości teoretycznych tej zmiennej, obliczonej na podstawie funkcji regresji. --- # Dopasowanie modelu **Współczynnik determinacji** określa, jaki procent wariancji zmiennej objaśnianej został wyjaśniony przez funkcję regresji. `\(R^2\)` przyjmuje wartości z przedziału `\(<0;1>\)` ( `\(<0\%;100\%>\)` ), przy czym model regresji tym lepiej opisuje zachowanie się badanej zmiennej objaśnianej, im `\(R^2\)` jest bliższy jedności (bliższy 100%) `$$R^2=1-\frac{\sum\limits_{i=1}^{n}{(y_{i}-\hat{y}_{i})^2}}{\sum\limits_{i=1}^{n}{(y_{i}-\bar{y}_{i})^2}}$$` Współczynnik determinacji przyjmuje wartości z przedziału `\(<0;1>\)` wyłącznie wtedy, kiedy został wykorzystany model oszacowany metodą najmniejszych kwadratów. W przeciwnym przypadku wartości tego współczynnika mogą być z przedziału `\((-\infty;1>\)`. --- # Dopasowanie modelu **Dopasowany współczynnik determinacji** ma na celu uwzględnienie i eliminację własności współczynnika determinacji polegającej na automatycznym zwiększaniu wartości `\(R^2\)` przy dodawaniu kolejnych cech do modelu. W tej formule uwzględnia się liczbę obserwacji oraz liczbę cech objaśniających: `$$\bar{R}^2=1-(1-R^2)\frac{n-1}{n-p-1}$$` Dopasowany współczynnik determinacji `\(\bar{R}^2\)` będzie zawsze mniejszy bądź równy wartości `\(R^2\)`. Może także przyjmować wartości ujemne. --- # Test Walda - sprawdzenie istotności parametrów `\(b\)` - sprawdzenie istotności całego wektora parametrów `\(b\)` --- # Inne miary jakości Do analizy jakości modelu można także wykorzystać inne miary obliczane na podstawie wartości rzeczywistych oraz predykcji. Te najpopularniejsze zaimplementowane są w pakiecie [mlr3measures](https://cran.r-project.org/web/packages/mlr3measures/). - MAE - Mean Absolute Error - MAPE - Mean Absolute Percentage Error - MSE - Mean Squared Error - RMSE - Root Mean Squared Error W pliku pomocy, dla każdej miary jest określony jej wzór, informacja o możliwych wartościach oraz kierunku pożądnych wartości (minimalizacja czy maksymalizacja). --- # Predykcja W celu wykorzystania modelu regresji do prognozowania należy stworzyć lub wczytać zbiór danych z danymi, dla których chcemy uzyskać wartości. ```r nowe_dane <- data.frame(x=c(10,20,30)) predict(object = model, newdata = nowe_dane) ``` --- # Trend liniowy W przypadku istnienia zależności liniowej w czasie, przedstawioną metodę można także wykorzystać do prognozowania wartości cechy w przyszłości. ```r df_trend <- data.frame(rok=c(2016, 2017, 2018, 2019, 2020), t=1:5, y=c(53, 55, 57, 56, 59)) knitr::kable(df_trend) ``` | rok| t| y| |----:|--:|--:| | 2016| 1| 53| | 2017| 2| 55| | 2018| 3| 57| | 2019| 4| 56| | 2020| 5| 59| --- # Sezonowość Dla danych charakteryzujących się występowaniem sezonowości należy skorzystać z metod, które to uwzględnią np. - [prophet](https://facebook.github.io/prophet/) - [ARIMA](https://fable.tidyverts.org/) - [TimeGPT](https://docs.nixtla.io/docs/getting-started-timegpt_quickstart) --- class: inverse # Zadanie Stwórz model regresji prostej objaśniający zależność sprzedaży od liczby klientów na podstawie [sklepu Rossmann](http://www.wawrowski.edu.pl/data/sklep77.xlsx). Jaka jest prognozowana sprzedaż dla 300, 700 i 1050 klientów? <div class="countdown" id="timer_d8e56e09" data-update-every="1" tabindex="0" style="top:0;right:0;"> <div class="countdown-controls"><button class="countdown-bump-down">−</button><button class="countdown-bump-up">+</button></div> <code class="countdown-time"><span class="countdown-digits minutes">10</span><span class="countdown-digits colon">:</span><span class="countdown-digits seconds">00</span></code> </div> --- # Regresja wieloraka Ogólna postać regresji wielorakiej jest następująca: `$$\hat{y}_{i}=b_{1}x_{1i}+b_{2}x_{2i}+...+b_{k}x_{ki}+b_{0}$$` W tym przypadku nie wyznaczamy prostej tylko `\(k\)`-wymiarową przestrzeń. 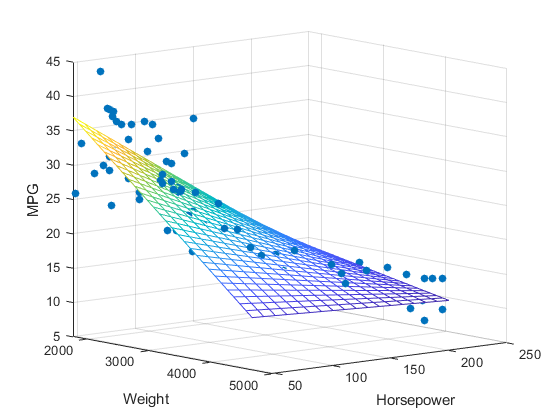--- # Regresja trzech zmiennych  --- # Przykład Na podstawie zbioru [pracownicy](http://www.wawrowski.edu.pl/data/pracownicy.xlsx) zbuduj model objaśniający wysokość bieżącego wynagrodzenia. - id - kod pracownika - plec - płeć pracownika (0 - mężczyzna, 1 - kobieta) - data_urodz - data urodzenia - edukacja - wykształcenie (w latach nauki) - kat_pracownika - grupa pracownicza (1 - specjalista, 2 - menedżer, 3 - konsultant) - bwynagrodzenie - bieżące wynagrodzenie - pwynagrodzenie - początkowe wynagrodzenie - staz - staż pracy (w miesiącach) - doswiadczenie - poprzednie zatrudnienie (w miesiącach) - zwiazki - przynależność do związków zawodowych (0 - nie, 1 - tak) - wiek - wiek (w latach) --- class: inverse # Zadanie Na bazie zbioru pracownicy stwórz nowy zbiór danych, który nie będzie zawierał niepotrzebnych zmiennych oraz braków danych. <div class="countdown" id="timer_c31371cb" data-update-every="1" tabindex="0" style="top:0;right:0;"> <div class="countdown-controls"><button class="countdown-bump-down">−</button><button class="countdown-bump-up">+</button></div> <code class="countdown-time"><span class="countdown-digits minutes">05</span><span class="countdown-digits colon">:</span><span class="countdown-digits seconds">00</span></code> </div> --- # Dychotomizacja zmiennej Zamiana zmiennej ilościowej zawierającej `\(k\)` wariantów na `\(k-1\)` zmiennych zerojedynkowych. .pull-left[ Oryginalny zbiór | id | stanowisko | |----|------------| | 1 | specjalista| | 2 | menedżer | | 3 | specjalista| | 4 | konsultant | | 5 | konsultant | ] .pull-right[ Zmienna zerojedynkowa | id | menedżer | konsultant | |----|----------|------------| | 1 | 0 | 0 | | 2 | 1 | 0 | | 3 | 0 | 0 | | 4 | 0 | 1 | | 5 | 0 | 1 | ] --- # Dychotomizacja zmiennej Współczynnik `\(b\)` dla zmiennej dychotomicznej informuje o ile przeciętne zmieni się wartość zmiennej objaśnianej `\(y\)` w odniesieniu do kategorii bazowej dychotomicznej zmiennej `\(x\)`. Przykładowo, przyjmując za kategorię bazową stanowisko _specjalista_, współczynnik `\(b\)` dla kategorii _menedżer_ poinformuje o ile średnio wartość bieżącego wynagrodzenia jest wyższa lub niższa od _specjalisty_. --- # Badanie współliniowości Pakiet [corrplot](https://cran.r-project.org/web/packages/corrplot/) służący do wizualizacji współczynnika korelacji. Współczynnik korelacji informuje o sile zależności pomiędzy dwoma cechami ilościowymi. Jest wielkością unormowaną, przyjmuje wartości z przedziału `\(r\in<-1;1>\)`. Jeśli: - `\(r_{xy}=1\)` - korelacja dodatnia doskonała, - `\(0<r_{xy}<1\)` - korelacja dodatnia niedoskonała (słaba/umiarkowana/silna) - `\(r_{xy}=0\)` - brak zależności, - `\(-1<r_{xy}<0\)` - korelacja ujemna niedoskonała (słaba/umiarkowana/silna) - `\(r_{xy}=-1\)` - korelacja ujemna doskonała. --- # Dobór i weryfikacja modelu Pakiet [olsrr](https://cran.r-project.org/web/packages/olsrr/) zawiera narzędzia do analizy modeli liniowych. - wybór cech do modelu - badanie współliniowości - badanie normalności - analiza wartości odstających --- # Dobór modelu Wyróżnia się trzy podejścia do tego zagadnienia: - ekspercki dobór cech - budowa wszystkich możliwych modeli i wybór najlepszego według określonego kryterium - regresja krokowa --- # Badanie współliniowości **Współczynnik tolerancji** wskazuje na procent niewyjaśnionej zmienności danej zmiennej przez pozostałe zmienne objaśniające. **Współczynnik VIF** jest obliczany na podstawie wartości współczynnika tolerancji i wskazuje o ile wariancja szacowanego współczynnika regresji jest podwyższona z powodu współliniowości danej zmiennej objaśniającej z pozostałymi zmiennymi objaśniającymi. Wartość współczynnika VIF powyżej 4 należy uznać za wskazującą na współliniowość. --- # Wartości odstające **Miara Cooka** jest obliczana poprzez usunięcie i-tej obserwacji z danych i ponowne obliczenie parametrów regresji. Podsumowuje, jak bardzo wszystkie wartości w modelu regresji zmieniają się po usunięciu i-tej obserwacji. Każda obserwacja, dla której wartość miary Cooka przekracza próg obliczany jako `\(4/n\)` jest traktowana jaka wartość odstająca. **Reszty studentyzowane** oblicza się, dzieląc resztę przez szacunkowe odchylenie standardowe. Odchylenie standardowe dla każdej reszty jest obliczane z wyłączeniem danej obserwacji. Obserwacje dla których wartość reszty przekracza 3 uznaje się za odstające. --- class: inverse # Zadanie Na podstawie zbioru dotyczącego [50 startupów](http://www.wawrowski.edu.pl/data/startups.xlsx) określ jakie czynniki wpływają na przychód startupów. Przyda się pakiet _janitor_ i funkcja `clean_names()` do uporządkowania nazw kolumn. <div class="countdown" id="timer_04784740" data-update-every="1" tabindex="0" style="top:0;right:0;"> <div class="countdown-controls"><button class="countdown-bump-down">−</button><button class="countdown-bump-up">+</button></div> <code class="countdown-time"><span class="countdown-digits minutes">10</span><span class="countdown-digits colon">:</span><span class="countdown-digits seconds">00</span></code> </div> --- class: inverse, center, middle # Pytania?