Metody przetwarzania i analizy danych

.title[
# Metody przetwarzania<br>i analizy danych
]
.subtitle[
## Testy statystyczne
]
.author[
### © Łukasz Wawrowski
]

---

# Testowanie hipotez

1. Sformułowanie dwóch wykluczających się hipotez - zerowej `\(H_0\)` oraz alternatywnej `\(H_1\)`

2. Wybór odpowiedniego testu statystycznego

3. Określenie dopuszczalnego prawdopodobieństwo popełnienia błędu I rodzaju (czyli poziomu istotności `\(\alpha\)`)

4. Podjęcie decyzji

---

# Wartość p

- najostrzejszy poziom istotności, przy którym możemy odrzucić hipotezę `\(H_0\)`

- podjęcie decyzji na podstawie porównania wartości p z poziomem istotności `\(\alpha\)`

- `\(p < \alpha\)` - odrzucamy hipotezę zerową

- [Rozważania o p-value](http://cejsh.icm.edu.pl/cejsh/element/bwmeta1.element.cejsh-e3daa053-7cf2-4eee-9192-16c48c3a7a45/c/05.pdf)

- [Oświadczenie Amerykańskiego Towarzystwa statystycznego o stosowaniu wartości p](https://idane.pl/post/oswiadczenie-amerykanskiego-towarzystwa-statystycznego-o-stosowaniu-wartosci-p-i-co-z-tego-wynika/)

]

![](img/freddie.jpg)

]

---

# Testy statystyczne

![](img/07_testy_diagram_v3.png)

---

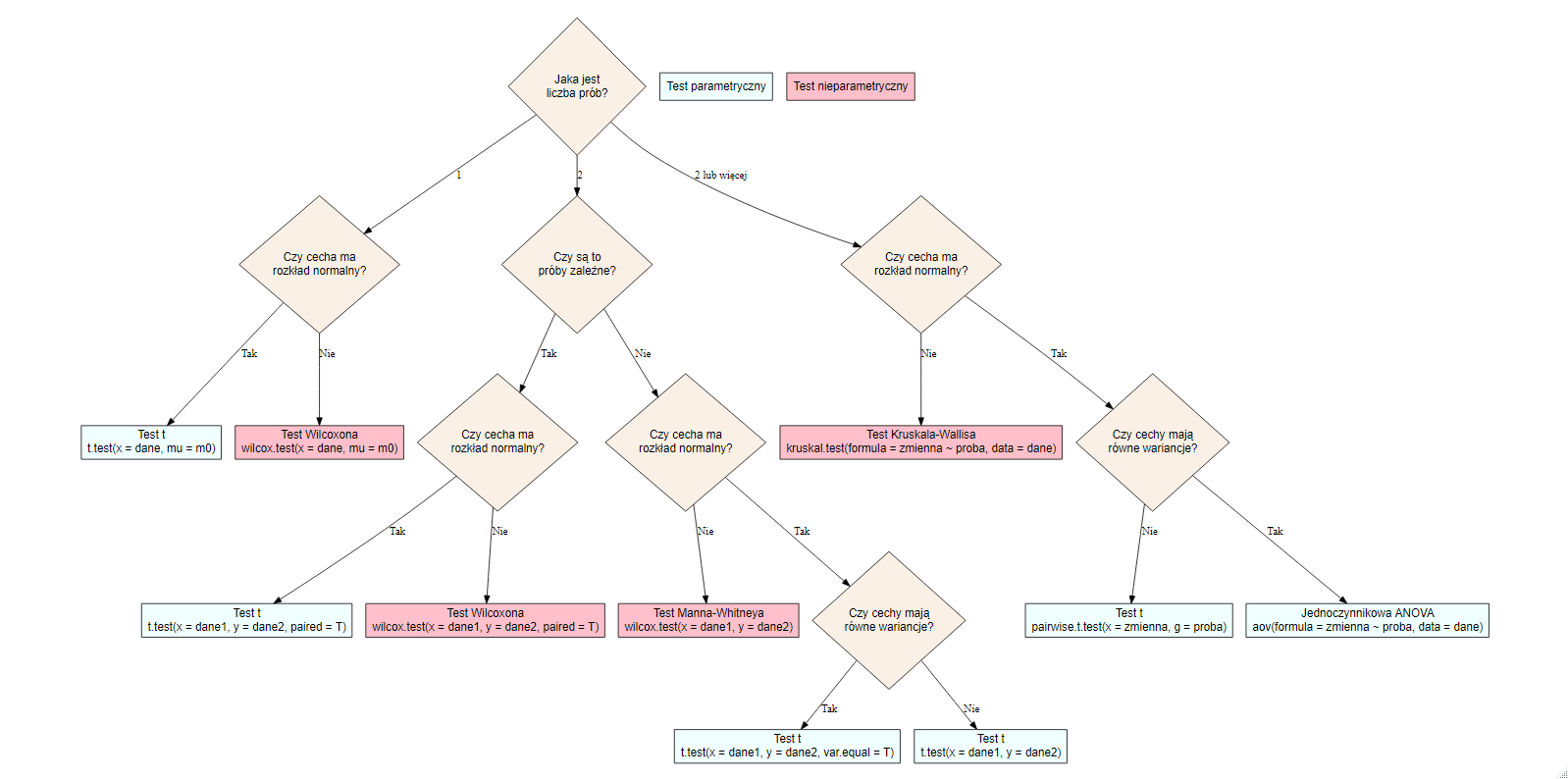
# Testy statystyczne

|                       | Skala nominalna - nieparametryczne | Skala porządkowa - nieparametryczne                  | Skala ilorazowa - parametryczne             |
|-----------------------|------------------------------------|------------------------------------------------------|---------------------------------------------|
| Jedna próba           | Test zgodności `\(\chi^2\)` - `prop.test()`     | Test zgodności Shapiro-Wilka - `shapiro.test()`, Test Wilcoxona - `wilcox.test()` | Test t - `t.test()`                   |
| Dwie próby niezależne | Test niezależności `\(\chi^2\)` - `chisq.test()`, Test zgodności `\(\chi^2\)` - `prop.test()` | Test Flignera-Killeena - `fligner.test()`, Test Manna-Whitneya - `wilcox.test()` | Test F - `var.test()`, Test t - `t.test()`                |
| Dwie próby zależne    | Test McNemara - `mcnemar.test()`     | Test Wilcoxona - `wilcox.test()`  | Test t - `t.test()`    |
| K prób niezależnych   | Test zgodności `\(\chi^2\)` - `chisq.test()` | Test Flignera-Killeena - `fligner.test()`, Test Kruskala-Wallisa - `kruskal.test()` | Test Bartletta - `bartlett.test()`, ANOVA - `aov()` |

---

[źródło](https://philipppro.github.io/Statistical_tests_overview/)

---

# Test niezależności `\(\chi^2\)`

Za pomocą testu niezależności `\(\chi^2\)` można sprawdzić czy pomiędzy dwiema cechami jakościowymi występuje zależność.

- `\(H_0:\)` zmienne są niezależne,

- `\(H_1:\)` zmienne nie są niezależne.

Funkcja `chisq.test()` z pakietu _stats_:

- tabela kontyngencji utworzona za pomocą funkcji `table()`

---

# Zadanie

Czy pomiędzy płcią, a grupami bieżącego wynagrodzenia zdefiniowanymi przez medianę istnieje zależność?

---

# Test proporcji

Test proporcji pozwala odpowiedzieć na pytanie czy odsetki w jednej, dwóch lub więcej grupach różnią się od siebie istotnie.

- `\(H_0: p_1=p_2\)`

- `\(H_1: p_1 \neq p_2\)` lub `\(H_1: p_1 > p_2\)` lub `\(H_1: p_1 < p_2\)`

Funkcja `prop.test` z pakietu _stats_:

- `x` - licznik badanych odsetków

- `n` - mianownik badanych odsetków

---

# Przykład

Wysunięto przypuszczenie, że palacze papierosów stanowią jednakowy odsetek wśród mężczyzn i kobiet. W celu sprawdzenia tej hipotezy wylosowano 500 mężczyn i 600 kobiet. Okazało się, że wśród mężczyzn było 200 palaczy, a wśród kobiet 250.

```r
prop.test(x = c(200,250), n = c(500,600))
```

```
## 
## 	2-sample test for equality of proportions with continuity correction
## 
## data:  c(200, 250) out of c(500, 600)
## X-squared = 0.24824, df = 1, p-value = 0.6183
## alternative hypothesis: two.sided
## 95 percent confidence interval:
##  -0.07680992  0.04347659
## sample estimates:
##    prop 1    prop 2 
## 0.4000000 0.4166667
```

---

# Zadanie

W pewnym powiecie na 119 przedsiębiorstw z sekcji PKD C i 174 z sekcji F w badaniu DG 1 wzięło odpowiednio 14 i 24 przedsiębiorstwa. Na poziomie istotności 0,05 zweryfikuj hipotezę, że odsetek przedsiębiorstw biorących udział w badaniu różni się pomiędzy sekcjami PKD.

---

# Test normalności

Najpopularniejszym testem jest test Shapiro-Wilka:

- `\(H_0: F(x) = F_0(x)\)` - rozkład cechy ma rozkład normalny

- `\(H_1: F(x) \neq F_0(x)\)` - rozkład cechy nie ma rozkładu normalnego

Funkcja `shapiro.test()` z pakietu _stats_:

- `x` - badana cecha

Maksymalna liczba obserwacji to 5000. Dla większej liczby test Kołmogorova-Smirnova (`ks.test()`) porównujący dwa rozkłady.

---

# Wykres kwantyl-kwantyl

```r
set.seed(128)

df <- data.frame(norm = rnorm(50))

ggplot(df, aes(sample = norm)) +
  stat_qq() + 
  stat_qq_line()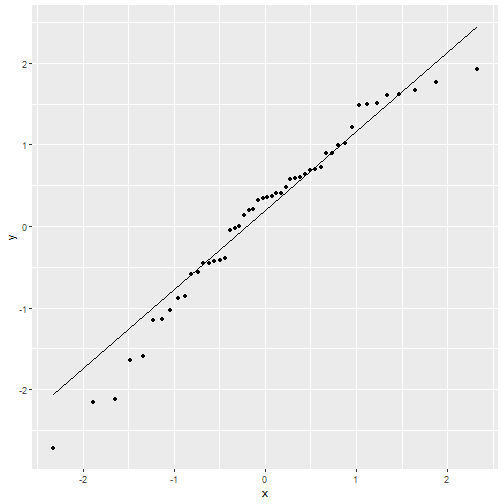 
```

]

![](03_testy_files/figure-html/unnamed-chunk-4-1.png)

]

---

# Zadanie

Czy cecha _bieżące wynagrodzenie_ ma rozkład normalny? Sprawdź za pomocą odpowiedniego testu oraz wykresu kwantyl-kwantyl.

---

# Test wariancji

Jeśli chcemy sprawdzić homogeniczność wariancji w więcej niż dwóch grupach to należy skorzystać z testu Bartletta:

- `\(H_0: s^2_1=s^2_2= s^2_3 =...=s^2_k\)`

- `\(H_1: \exists_{i,j\in\{1,..,k\}} \; s^2_i \neq s^2_j\)`

Funkcja `bartlett.test()` z pakietu _stats_:

- jako wzór z tyldą `zmienna_analizowana ~ zmienna_grupująca`.

---

# Próby zależne i niezależne

**Próby zależne (paired)**

Analizowane są te same jednostki, ale różne cechy.

**Próby niezależne (unpaired)**

Analizowane są różne jednostki, ale ta sama cecha.

---

# Test t-średnich

Porównanie wartości średnich:

- `\(H_0: m_1 = m_2\)`

- `\(H_1: m_1 \neq m_2\)` lub `\(H_1: m_1 < m_2\)` lub `\(H_1: m_1 > m_2\)`

Funkcja `t.test()`

- jako wzór z tyldą `zmienna_analizowana ~ zmienna_grupująca`

- `data` - zbiór danych

- `paired = TRUE` - dodatkowy argument dla prób zależnych

---

# Test Wilcoxona

Test Wilcoxona jest nieparametryczną wersją testu t.

- `\(H_0: F_1=F_2\)`

- `\(H_1: F_1 \neq F_2\)`

Funkcja `wilcox.test()` - argumenty takie jak w przypadku funkcji `t.test()`.

---

# Zadanie

Sprawdź czy wynagrodzenie różni się w zależności od płci.

---

# ANOVA

W przypadku większej liczby grup stosuje się jednoczynnikową analizę wariancji (ANOVA).

- `\(H_0: m_1 = m_2 = m_3 = ... = m_k\)`

- `\(H_1: \exists_{i,j\in\{1,..,k\}} \; m_i \neq m_j\)`

Funkcja `aov()`.

- wzór z tyldą `zmienna_analizowana ~ zmienna_grupująca`

- `data` - zbiór danych

Funkcja `TukeyHSD()` przeprowadza test post-hoc w przypadku istotnych różnic.

---

# Test Kruskala-Wallisa

Test Kruskala-Wallisa jest nieparametrycznym odpowiednikiem ANOVA.

- `\(H_0: F_1=F_2=F_3=...=F_k\)`

- `\(H_1: \exists_{i,j\in\{1,..,k\}} \; F_i \neq F_j\)`

Funkcja `kruskal.test()` - argumenty takie jak w przypadku funkcji `aov()`.

---

# Zadanie

Sprawdź czy wynagrodzenie różni się w zależności od kategorii pracownika.

---

# Pytania?